Polynomials

U н я л е р с я т у

                       S щ е т ш т е

                         МНОГОЧЛЕНЫ

                          СИНКЛЕР

                    ZX Spectrum (16K-48K)

                  Программы, составляющие

            U н я л е р с я т у с о е т ш а р е

 БИБЛИОТЕКА Продвинутые математические / STAT / ECON были тщательно

 подготовленный командой аспирантов из Университета  из Лондона. Хотя программы предназначены для обработки  самые сложные проблемы, инструкции напечатаны на  охватывает намерены ввести неспециалисту в  Основы теории.

 Все программы начинают выполнение автоматически, как только они  загружен и все, что требуется, это следовать инструкциям  ции отображаются на экране. Но, используемый не отрицается  право доступа к программе списков. REM  заявления дать пользователю представление о том, как они работают. Если  сокращение времени выполнения или требуется больше пространства памяти,  они могут быть исключены из программ.

? Copyright 1983

            U н я л е р с я т у с о е т ш а р е

             29 Санкт-Питерс-стрит, Лондон N1 8JP

Никакая часть этой записи, ее листинги программ или

Содержание этой кассеты инкрустации могут быть воспроизведены без письменное разрешение. Хотя все должные меры были приняты в подготовке этих программ, издатель не несет ответственности за любые ошибки или ответственность за любой ущерб, причиненный их

использовать.

Сторона: вещественность В.

Полином является функция вида:

             N N-1 2    F (х) = с х + с х +. , с х + с х + с            N N-1 2 1 0

где сп c0 называются коэффициентами и н Степень полинома. Значения х, которые удовлетворяют F (X) = 0 называются корни многочлена.

Для расчета корни Настоящая программа использует три

различными методами.

(Я) Квадратные уравнения являются на самом деле второй степени поли-

номы. Если степень полинома вводится 2, в Корни рассчитывается по формуле:                                                         _ / 2                       -с + / с – 4с с                       __1_V__12_0___                                2с                                  0

(Б) Ньютона-Рафсона Метод применяется в более высокой степени (3 или

больше) многочлены. Основной шаг метода заключается в следующим образом: начиная с произвольно выбранной исходной величины х (скажем x0), еще х (говорят x1) производится которая ближе любому из корней функции F (X). x1 производится по формуле:

                                F (х)

                     х = х – 0__                       1 0 F ‘(х)                                     0

где F (x0) является значение первой производной F (х) для х = х0. Конечно, мы предполагаем, что F (х) дифференцируема. Это шаг повторяется до разницы между новым х и старый х меньше желаемой степенью точности. В эта программа этого уровня точности устанавливается как 10 ^ -8. Если F (х) делает не имеет реальных корней, итерация выполняется 100 раз. Опция итерации еще 100 раз доступно.

Если один корень найден, другие корни можно искать по

ввода различных начальных значений. Хотя Ньютона-Рафсона метод приближения работает гораздо быстрее, чем наполовину интервальный метод поиска, трудно угадать, какая начальная стоимость приблизительно в которых корень.

(III) Half-интервальный метод поиска ищет изменению знака из F (X) в пределах данного интервала. Первый интервал разделен на 10 равных частей и изменение знак искали Эти приращения. Если изменение знака встречается пределы текущий прирост определяется как нового интервала и в повернуть делится на 10 этапов. Эта процедура повторяется до тех пор, пока приращение меньше 10 ^ -8. Если никаких изменений знак не является найдено в первые 10 итераций, первоначальный интервал разделен в 100 с шагом и поиска повторяется. Если до сих пор нет никаких признаков Изменение найден отсутствие действительных корней в данный Интервал сообщается.

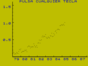
Сторона Б: УЧАСТОК ПОЛИНОМОВ

Эта программа строит полиномы между заданных пределах,

печатает значения экстремума и нижние и верхние пределы на осях. Если корень найден х оси регулирует свое местоположение в соответствии со значениями полинома и приблизительное значение корня печатается в точке пересечения.

Желательно, чтобы использовать эту программу сначала иметь представление

о поведении материала полинома, а затем использовать Side A

определить точные значения корней.

 U S МНОГОЧЛЕНЫ

 УНИВЕРСИТЕТ

  ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ

Библиотека

Продвинутый Математика / Stat / Econ:

MATRIX

ОПЕРАЦИИ

МНОГОЧЛЕНЫ

ИНТЕГРАЦИЯ

РЕГРЕССИЯ

ЛИНЕЙНАЯ

Программирование